カイ二乗値

カイ二乗値（Χ²値）は、クロス集計表などで算出する数値で、変数間での関連性がないと仮定した状態からの乖離、期待度数からの乖離を表す指標です。ピアソンのカイ二乗統計量、適合度統計量ともいいます。

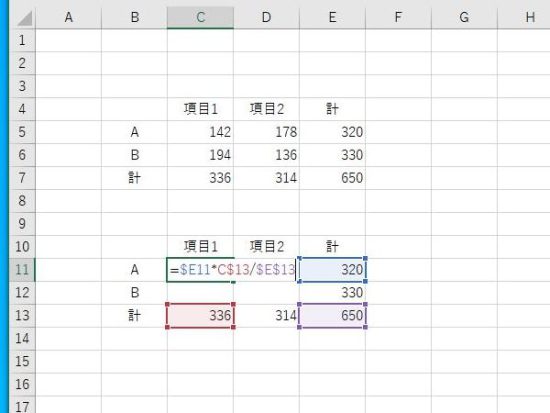
C11に数式を入力。期待度数は 行合計×列合計/総度数で求めます。

B4:E7に実測度数（観測度数）の表、B10:E17に期待度数の表。期待度数の表における周辺度数（行・列の合計）と総度数は、実測度数と同じ数値になります。

数式は四則演算を使います。個別にセルを計算する、行ごとや列ごと計算する、複合参照で行と列を計算するなどの方法があります。この例では、$E11*C$13が複合参照、$E$13が絶対参照となります。

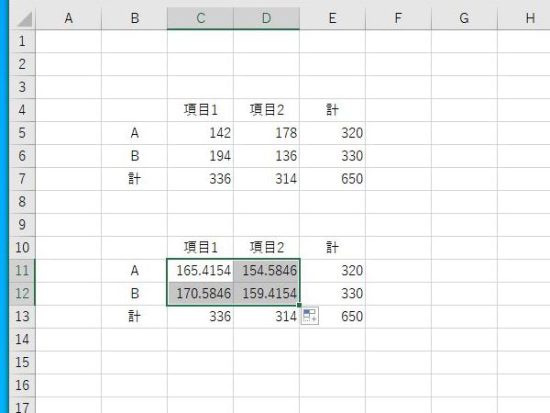
オートフィルの結果。期待度数が表示されます。

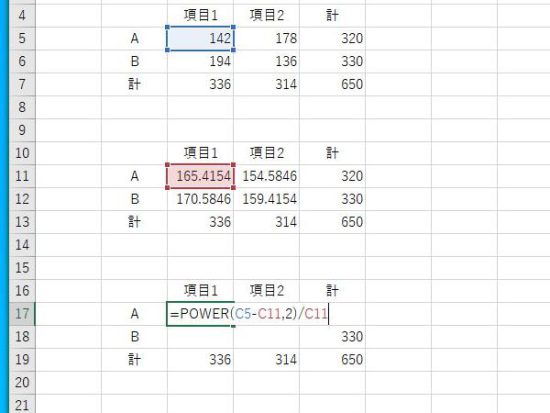
B17に数式を入力。Χ²値は (実測度数-期待度数)²/期待度数で算出することができます。2乗はPOWER関数を使います。

3つとも行・列が同じ表であるため、B17の数式内のセルは C5-C11やC11のように入力することで相対参照で計算が行われます。

各セルごとに数値が表示されます。

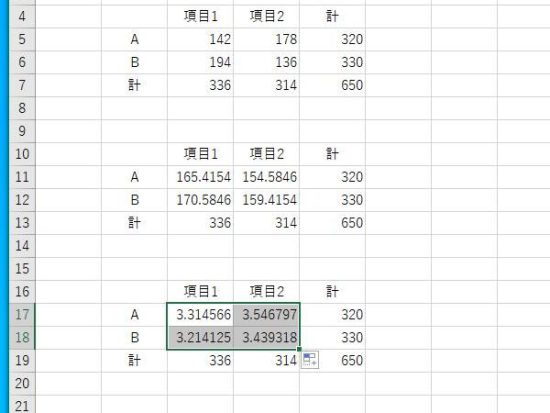
B21にSUM関数を入力。数値を合計します。

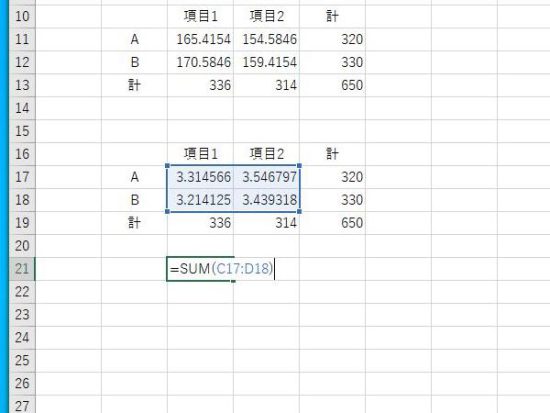
Χ²値が表示されます。

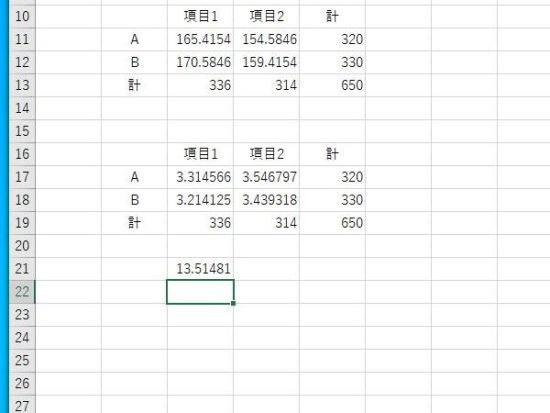
期待度数とΧ²値の数式。

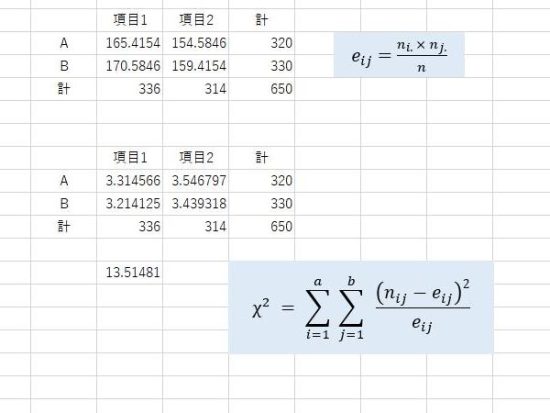
まとめると、Χ²値は以下の方法で求めることができます。

1. 各セルの期待度数の算出・・行合計×列合計/総度数
2. 各セルの数値の算出・・(実測度数-期待度数)²/期待度数
3. 各セルのΧ²値の合計・・2の合計

Χ²値を求める場合は、実測度数の表とは別に 期待度数の表、各セルのΧ²値の表を作ると計算を行いやすくなります。実測度数と期待同数の数値が全く同じ場合は、Χ²値は0となります。

Χ²値が大きければ、関連性があると考える要因にもなります。ただΧ²値は、データや行列の数によって大きさも変化するため、単純に数値のみで判断できるわけではありません。

Χ²値は、カイ二乗検定（カイ二乗分布表の使用やp値）、クラメールの連関係数などで使われます。