RSQ関数(決定係数・寄与率)
コリレーション・スクエア
RSQ関数は、決定係数を返す関数です。決定係数とは、回帰直線の予測の精度・適合度を示す指標で、0~1の値をとり XによってYがどのぐらい(何%)説明できるか表しています。寄与率ともいいます。
決定係数は、R2と表記され R2=1のときは、完全な相関関係にあり XによってYを完全に予測できる、一方 R2=0のときは、無相関でありXからYを予測することはできないということになります。
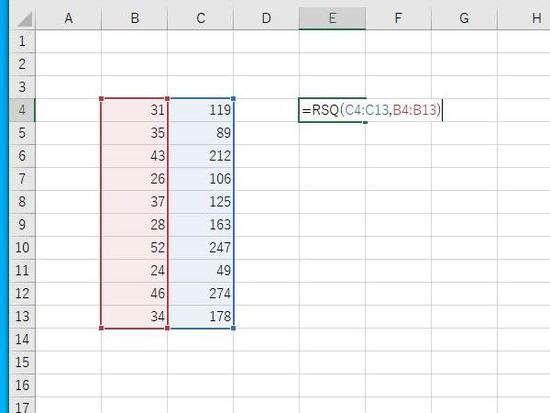
例:RSQ関数を入力。第1引数にyのデータ範囲(C列)、第2引数にxのデータ範囲(B列)。yの次にxの範囲を指定します。
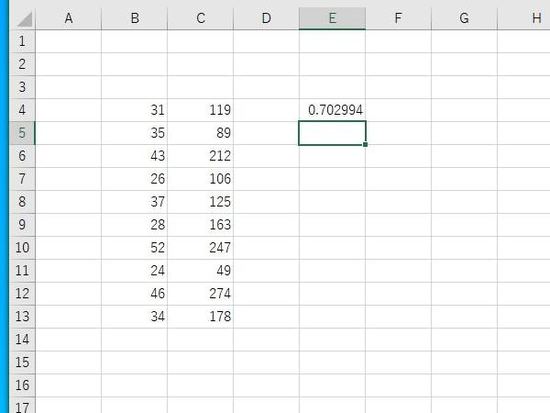
Enterで結果が表示されます。決定係数は、0.702994となります。小数点第6位まで表示。
決定係数は、RSQ関数以外でも求めることができます。
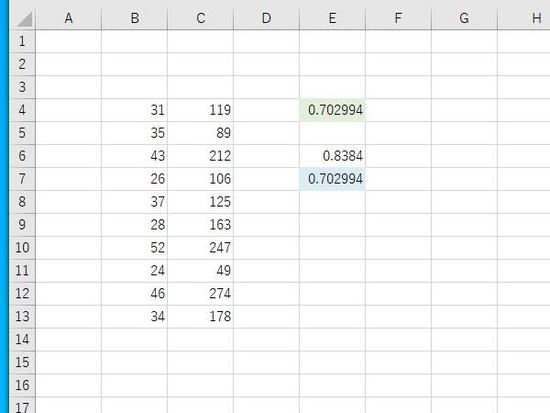
まず、相関係数の2乗があります。関数名であるRSQは、Correlation Square(Square of Correlation)の略で 相関係数の2乗を意味します。
E6に相関係数、E7に相関係数の2乗。相関係数はPEARSON関数かCORREL関数、2乗はPOWER関数、あるいは相関係数×相関係数のようにします。E4の関数の結果と一致します。
次に、決定係数の数式があります。
B14とC14に配列の平均、D列にy(C列)の偏差、E14に偏差平方和、F列に回帰式からの予測値、G列に予測値からの残差、H列に残差の2乗、H14に残差の2乗の和。
E14を全平方和 ST、H14を残差平方和 SE、全平方和-残差平方和を回帰平方和 SRといいます。H16に回帰平方和。
最後に回帰平方和÷全平方和、H16/E14で決定係数となります。H17に数式による決定係数、J4の関数による決定係数と一致します。
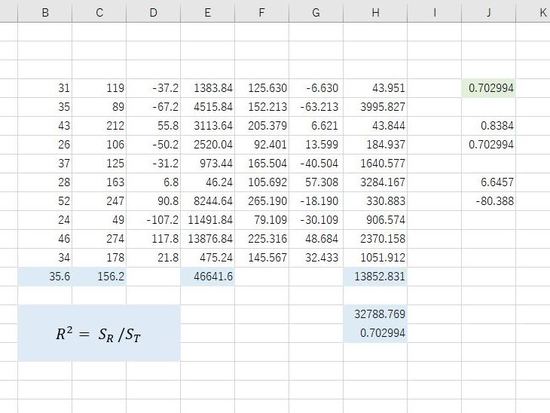
数式によって求める場合は、回帰式(予測式)と残差(予測値からのズレ)が必要です。
この例では、J9にSLOPE関数による回帰係数、J10にINTERCEPT関数による切片を表示しています。つまり、回帰式は y=6.6457x-80.388となります。
F列には、xの値を代入する式 =J$9*B4+J$10を入力します。回帰係数にxの値を掛けて切片を足します。オートフィルを行うと予測値が表示されます。
G列には、yの値から予測値を引く式 =C4-F4を入力します。オートフィルを行うと残差が表示されます。H列で2乗するため、G列の符号はあまり関係なく 予測値からyの値を引く式 =F4-C4でも問題ないといえます。
決定係数は、他にグラフでも表示させることができます。
2組のデータを選択して、挿入→グラフ、散布図。プロットされた点をクリックして選択し右クリック、近似曲線の追加→線形近似、数式とR-2乗値を表示。
回帰直線と回帰式、R2(決定係数)が表示されます。E3の関数の結果(小数点第3位まで表示)と一致します。この例では、ともに0.703となります。
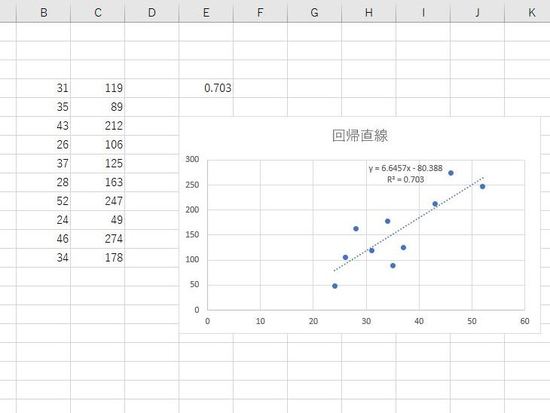
単回帰分析において、決定係数は予測の精度を示します。
一般的に相関係数が高いほど、決定係数は1に近い、予測の精度が高いといえます。例えば、相関係数が0.9であれば 決定係数は0.81、相関係数が0.2であれば決定係数は0.04のようになります。負の相関でも同様で、相関係数が-0.8であれば 決定係数は0.64、相関係数が-0.3であれば決定係数は0.09となります。
決定係数が0.81であれば、独立変数 Xによって 従属変数 Yは 81%説明できる、残りは他の要素に関係していると解釈することができます。