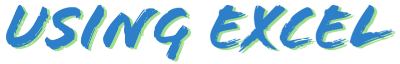INTERCEPT関数（回帰直線の切片）

インターセプト

INTERCEPT関数は、2組のデータから回帰直線の切片を返す関数です。

回帰直線とは、y=bx+a または y=a+bxの式（予測式）で表される直線で、bxのbを回帰係数、aの定数部分を切片といいます。

例：INTERCEPT関数を入力。第1引数にyのデータ範囲（C列）、第2引数にxのデータ範囲（B列）。yの次にxの範囲を指定します。

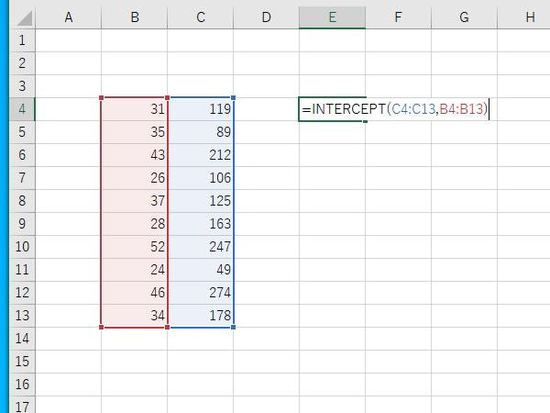
Enterで結果が表示されます。切片は -80.388となります。ホーム→数値、小数点第3位まで表示。

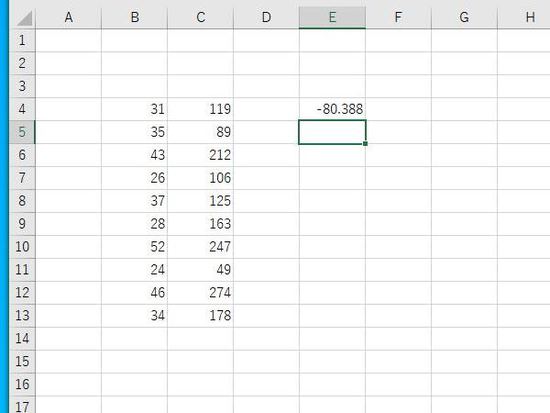
切片の数式。B14・C14に配列の平均、E14に回帰係数。数式にyの平均、xの平均、回帰係数を代入すると切片を算出することができます。E16に数式による切片、E4の関数による切片と一致します。

2組のデータを選択して、挿入→グラフ、散布図。プロットされた点をクリックして選択し右クリック、近似曲線の追加→線形近似、数式とR-2乗値を表示。

回帰直線と回帰式（予測式）が表示されます。切片はINTERCEPT関数と一致します。R²は 決定係数。

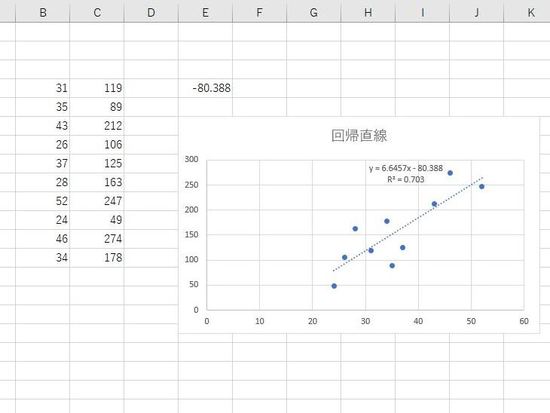
切片は、xが0のときに yのとる値になります。この例では、xが0のとき yは-80.388となります。

ただ回帰式・回帰直線を用いた単回帰分析では、xは現実的な数値データを入力するため、xに0やマイナスの数値を入力するというのはほとんどありません。切片は、回帰係数のある bxを補正するかたちではたらくものとなります。

単回帰分析では、回帰係数と切片を算出する必要がありますが、Excelでは上記のグラフのように データを選択して表示させると、回帰式（回帰係数と切片）が算出されます。そのため、SLOPE関数やINTERCEPT関数を必ず使うというわけではないといえます。