2進数

コンピューターの世界では、すべてのデータを2進数で表しています。2進数というのは、1桁で 0か1を使い表現しています。

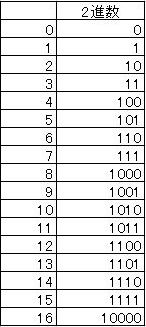左は普段使う10進数。

0は0、1は1です。

2進数の1桁では、0か1なので 2通りになります。このコンピューターのデータ最小単位を 1ビットといいます。

0と1の数字の組み合わせ・並びをビット列といいます。

コンピューターで2進数が使われるのは、0と1の2通りがあれば、ONかOFFか、電圧が強いか弱いかの電気信号に対応させて扱うことができるからです。

1ビットでは2通りしか表せませんが、ビット数が増えると表現できるものが増えてきます。

コンピューターの世界では、1ビットを8つ並べた 8ビットを 1バイトとしています。2進数で8桁になります。8bitをひとまとまりとして オクテットということもあります。この 8bitというのは、最も基本的な単位として用いられます。

8bitで表せるのは 2の8乗で0～255までの256通りになります。

ネットワークの規格であるイーサネットの速度を表すbpsでビット、メモリーやHDDなどの容量を表す単位でバイトが使われています。

2進数は、桁が上がれば それだけ表せるデータの量が増えることになります。

• 2の32乗・・4,294,967,296
• 2の64乗・・18,446,744,073,709,551,616

CPUやOSの32bitや64bitというのは、端的にいえば一度に処理できるデータの幅や量になります。ビット幅ともいいます。

ビット幅が大きいと、それだけ一度に多くの処理を行うことができ、速度も向上します。CPUやOSというのは、8bit→16bit→32bit→64bitと進化してきています。

コンピューターは、色も2進数で表現します。

例えばオレンジなら、11111111.10100101.00000000、のようになります。

• 2の24乗・・16,777,216

16,777,216通りの組み合わせがあります。

ディスプレイは、ドットやピクセルという点で構成されています。このひとつのドットに何ビットの情報をもたせているかで表示できる色の種類が決まります。

• ハイカラー・・1ドットに16bit、65,536色
• フルカラー・・1ドットに24bit、16,777,216色

現在のディスプレイの多くは、24bit フルカラーとよばれるものです。パソコンやディスプレイで使われるRGBは、24bitで色彩を表現しています。

コンピューターは、文字も2進数で表現します。

例えば 「あ」なら、1100000.1000010、「T」なら、1010100、など。

2進数の数字と、文字やアルファベット・記号を対応させたものを、文字コードといいます。この組み合わせ表を利用して、パソコンの画面上に文字や記号を表示させることができます。

文字コードは 8bit（1バイト）、16bit（2バイト）などで作られています。

• 8bit、2の8乗・・・256通り
• 16bit、2の16乗・・・65,536通り

8bitのものとして ASCII、16bitのものとして Shift_JISなどがあります。

アルファベットを用いる英語圏などでは ASCIIでも対応できますが、日本語のように、ひらがな、カタカナ、漢字など文字の種類が多い場合は、16bitは必要になります。様々な言語に対応した 4バイトのUTF-8などもあります。

コンピューターの世界では 2進数が使われますが、これをそのまま表記していたら分かりづらくなります。そのため、普段使うもののいくつかは 2進数が10進数に変換されて表記されています。

代表的なものには IPアドレスがあります。

例えば 192.168.1.1というプライベートIPアドレスがあるとします。これは 8bitが4つのオクテットに分かれ 32bitになっています。

2進数では、11000000.10100100.00000001.00000001、となります。しかしこの表記では分かりづらいため、2進数を10進数に変換して表記しています。

16進数は 0～9、A～Fの16種類の数字とアルファベットで表記します。

1桁で16種類、16通り表現できます。

16進数ということが分かるように、数字の先頭に 0xと付けることがあります。Windowsのエラーコードが、0xで始まっていますが 16進数で示しているということになります。

他に、カラーコードといわれるものがあります。HTML言語などで 線や文字の色を表現する際に使います。例えば白なら、#FFFFFF、オレンジなら、#FFA500、などです。先頭にハッシュ記号という #を付け 16進数で表記されます。

文字コードやMACアドレスも 2進数では分かりづらいため、実際は16進数で表記されています。

2進数は 1桁で0と1の2個、10進数は 1桁で0～9の10個、16進数では 1桁で0～9とA～Fの16個の数や記号を使います。

つまり、n進数では n個の数を使います。このnを 基数といいます。器をイメージします。2進数なら2個、10進数なら10個、16進数なら16個入ります。そしてそれ以上入らなくなれば、次の桁へ上ります。

桁数によって何通り表現されるか？何通りの組み合わせが実現できるかは、n進数に桁数を掛け合わせます。

例えば2進数で4ビットなら 2⁴ で16通り、8ビットなら 2⁸ で256通りです。同様に、10進数の4桁なら10⁴、16進数の3桁なら16³で何通りの組み合わせか計算できます。

ここからは、10進数、2進数、16進数の相互変換についての説明になります。情報処理の試験などでは、必ずといっていいほど出てくる問題です。

10進数を2進数にするときは、10進数の数字を2で割っていきます。最後割り切れない数字、1になるまで2で割っていき、余りを出していきます。

最後の1から並べたものが、2進数になります。

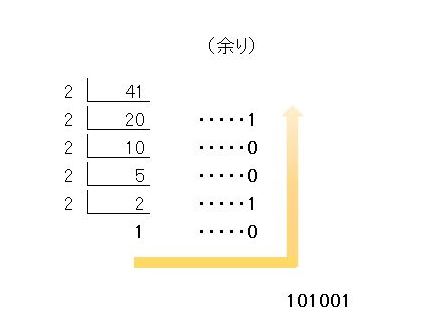
41を2で割ると、20と余り1です。次に20を2で割ると10と余り0です。これを繰り返していきます。最後の数字は必ず1になります。

つまり、最後は3を2で割って1余り1、もしくは 2を2で割って1余り0のいずれかになります。必ず11～か10～で始まります。

10進数を16進数にするときは、2進数のときと同じように今度は16で割っていきます。割り切れない数字、16未満になるまで、余りを出していきます。

最後の数字から並べると16進数になります。

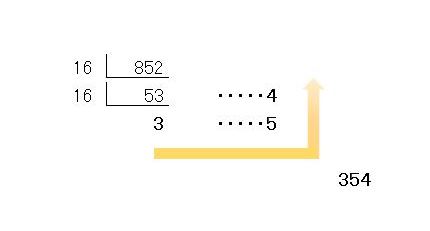
852を16で割ると、53余り4です。53を16で割ると、3余り5です。最後割り切れない数字から354が16進数になります。

16進数では、余りが10や15になるときがありますが、この場合 10ならA、15ならFになります。

次によく出てくるのが、2進数から10進数への変換です。

右から、2⁰、2¹、2²、2³と覚えておきます。

2⁰は、1になります。正の整数の0乗は1という決まりがあります。これは数学で定義されています。

右から、1、2、4、8・・と2の指数計算を行い、各桁の数字と掛け合わせます。合計をすべて足し算すると10進数の数字になります。

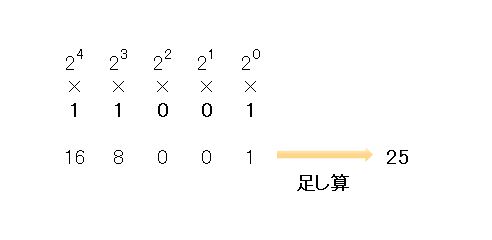
2進数を16進数に変換するという場合は、2進数を10進数にしてから16進数にするという方法がとられます。

例えば、上記のように 11001という2進数は10進数で25です。これを16で割っていき16進数にします。そうすると1、余りは9となり、19が16進数です。

2進数の桁数が多いときは、2進数を4桁づつで区切ります。2進数の4桁というのは、16通りの組み合わせで16進数の1桁に当てはまります。

一番右から4桁づつで区切り、3桁残ったりしたら 先頭に0を追加します。

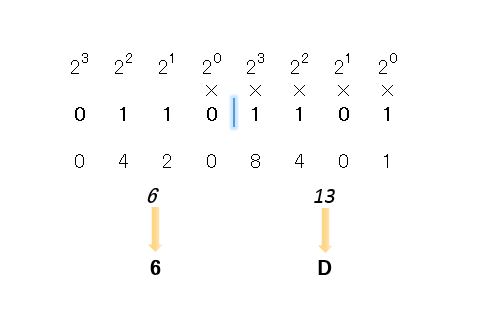
それぞれのブロックで、10進数を出し、これを16進数へ変換します。

10進数を求めるときは、ブロックで分けず5桁目から 2⁴、2⁵・・とするので、10進数では、6+13ではなく 109です。あくまで16進数を求める時だけ区切って計算します。

2⁰、2¹、2²、2³というような、指数計算の並びが思い出せない場合は、単純に10進数ではどうなっているかを考えます。

例えば、10進数の168があるとします。これは、10⁰×8、10¹×6、10²×1を足したもの、つまり 8+60+100で168となることが分かります。これを一般的に 位取り記数法といいます。

16進数は、2進数→16進数で説明したように 16進数の1桁が2進数の4桁にあたります。

そのため16進数が出てきたら、1桁が2進数の4桁になることをイメージします。

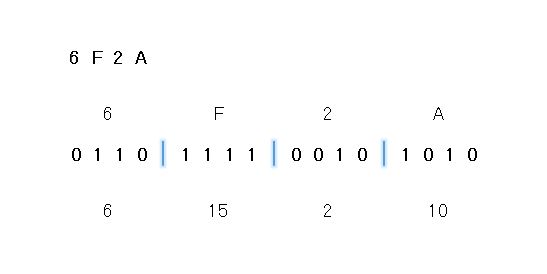
2進数は、0000～1111までが、10進数の0～15、16進数の0～Fになります。16進数は、0～9までは10進数と同じです。

2進数が分からないという場合は、一度10進数にして、10進数→2進数の2で割っていく方法をとれば、2進数は出せます。

例えば、Aは 10進数で10、2進数で1010になります。2は 10進数でも2、2進数で0010となります。4桁あるため00は省かないようにします。

すべて変換すると16進数の6F2Aは、2進数では、110111100101010になります。先頭の0は省きます。

16進数から10進数にする場合は、2進数→10進数と同じような方法です。

16進数の6F2Aなら、各桁を10進数にして、1桁目から16⁰、16¹、16²、16³・・・と掛けていきます。

出た数字をすべて足したものが、10進数の数字になります。16進数の6F2Aは 10進数では、28458になります。

10進数では負の数を表す際に、-2のようにマイナスの符号を付けます。

2進数で負の数を表す場合は、固定長のビット列が前提となります。例えば、2進数の10（10進数の2）は、4ビット固定長では、0010となります。

2進数で負の数を表す場合は、ビットを反転させて 1を足すということをします。

つまり、0010を反転させて1101、1を足して1110です。2進数の10の負の数は 4ビット固定長では 1110となります。補数表記、符号あり整数といいます。

実際のコンピューターでは、8ビットが最小単位として使われることから、情報処理のテキストなどでは、8ビット固定長における補数表記で解説されていることが多くなっています。

2進数の基礎的な項目としては、ビット、バイト、組み合わせの総数、2進数・10進数・16進数の相互変換、位取り記数法などです。

やや専門的な項目としては、負の数の他、2進数における小数、四則演算などがありますが、ここでは割愛しています。

Excelには、2進数・10進数・16進数の数値を変換する関数があります。

• DEC2BIN関数・・・10進数→2進数変換
• DEC2HEX関数・・・10進数→16進数変換
• BIN2DEC関数・・・2進数→10進数変換
• BIN2HEX関数・・・2進数→16進数変換
• HEX2BIN関数・・・16進数→2進数変換
• HEX2DEC関数・・・16進数→10進数変換
• BASE関数・・・10進数→n進数変換
• DECIMAL関数・・・n進数→10進数変換

Windowsには電卓のアプリケーションが付いています。

電卓を起動させて、メニューからプログラマーを選択。

HEXは16進数、DECは10進数、OCTは8進数、BINは2進数。例えば、DEC 10進数を選択して、10と入力すると、HEX 16進数にA、BIN 2進数に1010と表示されます。

10進数 25、2進数 00011001。表示方法をBYTE。

符号を付けることで、2進数の符号あり整数 11100111が表示。

2進数、10進数、16進数の適当な数字を紙に書いて変換してみて、電卓で答え合わせをするということができます。