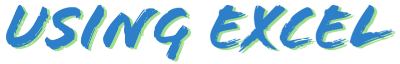STDEV.S関数（標本標準偏差）

スタンダード・ディビエーション・エス

STDEV.S関数は、データの標本標準偏差を返す関数です。標準偏差とは、データのばらつきの大きさを表す指標です。

一般的に母集団の標本データの標準偏差を算出する際に用いられます。STDEV.SのSは標本 sampleの意味。

例：STDEV.S関数を入力。引数にセル範囲を指定。

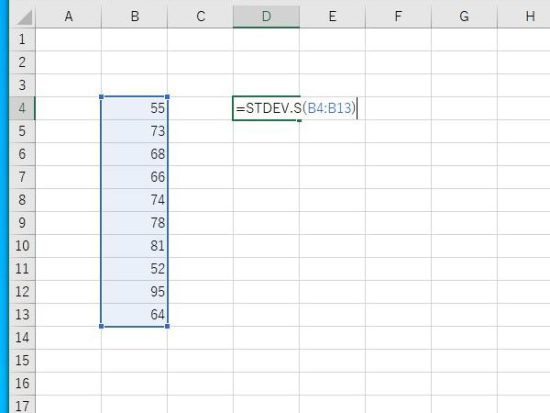
Enterで結果が表示されます。標本標準偏差は12.63329となります。小数点第5位まで表示。

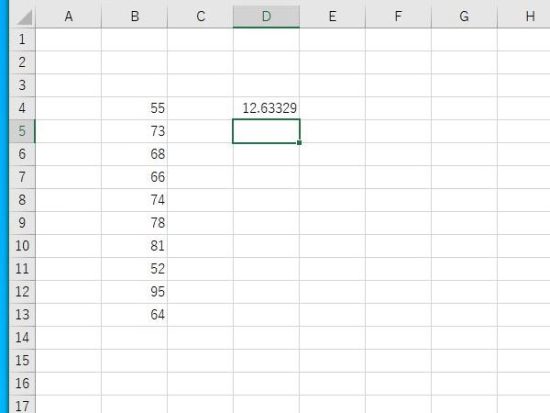
標本標準偏差の公式。B14に平均、D列に偏差、E14に偏差平方和、E16に不偏分散、E17に不偏分散の平方根、G4の関数による標準偏差と一致します。

まとめると、標本標準偏差は以下の方法で求めることができます。

1. データの値から平均値を引く（偏差）
2. 1を2乗
3. 2乗した数値をすべて足す（偏差平方和）
4. 3を（データの個数-1）で割る（不偏分散）
5. 4の平方根

不偏分散の算出方法と同じですが、標本標準偏差は最後に不偏分散の平方根で求めることができます。

標準偏差は、そのデータが母集団のデータか、母集団の標本データかによって使い分けられます。前者は標準偏差といい分散の平方根で算出します。一方 後者は、区別するために標本標準偏差といい不偏分散の平方根で算出します。

ただ、特に区別されずに標本標準偏差を標準偏差ということもあるため、文脈や数式の平方根の対象（分散・不偏分散）などで判断することもあります。

標本標準偏差は、不偏分散と同様に 母集団から標本をとり 母集団の傾向などを確認・分析する推測統計などで主に使われています。

STDEV.S関数と類似した関数に、STDEV.P関数があります。STDEV.S関数は 平方根の対象が不偏分散です。一方 STDEV.P関数は 平方根の対象が分散となります。