STDEV.P関数(標準偏差)
スタンダード・ディビエーション・ピー
STDEV.P関数は、データの標準偏差を返す関数です。標準偏差とは、データのばらつきの大きさを表す指標です。
一般的に母集団のデータ、標本ではないデータの標準偏差を算出する際に用いられます。STDEV.PのPは母集団 populationの意味。
例:STDEV.P関数を入力。引数にセル範囲を指定。
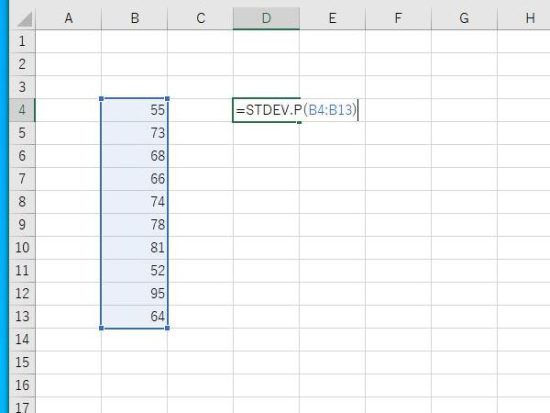
Enterで結果が表示されます。標準偏差は11.98499となります。小数点第5位まで表示。
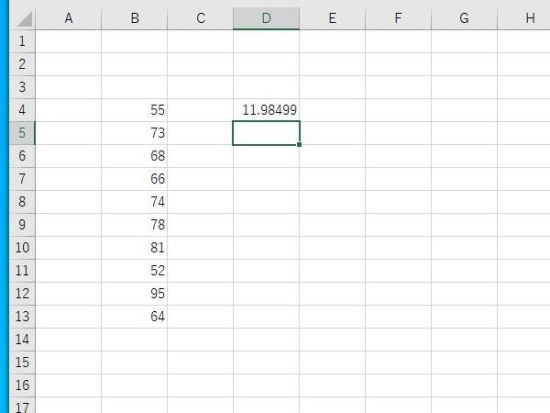
標準偏差の公式。B14に平均、D列に偏差、E14に偏差平方和、E16に分散、E17に分散の平方根、G4の関数による標準偏差と一致します。
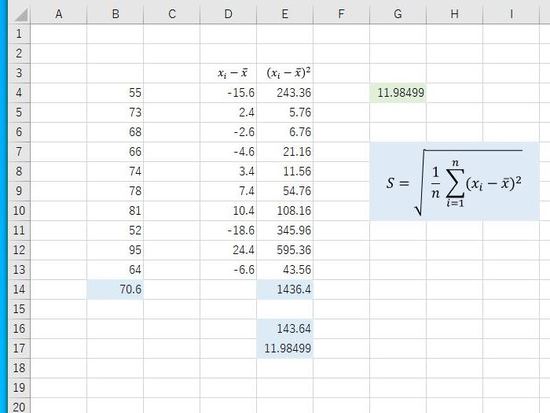
まとめると、標準偏差は以下の方法で求めることができます。
- データの値から平均値を引く(偏差)
- 1を2乗
- 2乗した数値をすべて足す(偏差平方和)
- 3をデータの個数で割る(分散)
- 4の平方根
分散の算出方法と同じですが、標準偏差は最後に分散の平方根で求めることができます。
標準偏差は 文字通り標準的な偏差を意味します。偏差とは データと平均の差です。標準偏差から そのデータの持つばらつきの大きさを知ることができます。
例えば、平均点が同じ75点のデータが2つあるとします。ひとつは標準偏差25、もうひとつは標準偏差10であるとすると、標準偏差25の方が点数にばらつきがある、標準偏差10の方は、平均に近いところにデータがまとまっているとなります。また、分散には単位はありませんが、標準偏差には平均と同様に単位があるのが特徴です。
標準偏差は、Standard Deviationの文字から S.D.、s、またsのギリシャ文字からシグマ、σと表記されることがあります。平均・中央値・最小値・最大値などと並び代表的な要約統計量、基本統計量のひとつとなります。
STDEV.P関数と類似した関数に、STDEV.S関数があります。STDEV.P関数は 平方根の対象が分散です。一方 STDEV.S関数は 平方根の対象が不偏分散となります。