ド・モルガンの法則

論理演算の法則に、ド・モルガンの法則があります。ド・モルガンの法則は、以下の2つの等式になります。

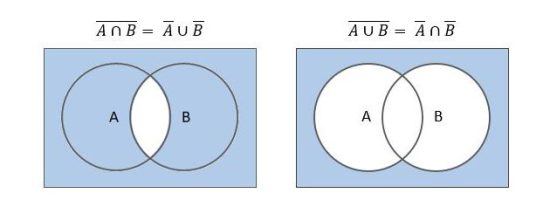
左側は (AかつB)ではない＝(Aではない)または(Bではない)、右側は (AまたはB)ではない=(Aではない)かつ(Bではない)となっています。左側を法則1、右側を法則2とよばれることもあります。

ド・モルガンの法則は、ANDとORは NOTを使うことで書き換えができるということを表しています。

これは Excelでも確認することができます。

例えば 1～10までの数字があり、Aに該当するものを2の倍数、Bに該当するものを3の倍数とします。

2の倍数と3の倍数を剰余で表すため、ここではMOD関数を使います。除数2で剰余0なら2の倍数、除数3で剰余0なら3の倍数となります。それぞれの論理式で該当するものは 真・TRUE、該当しないものは 偽・FALSEとなります。

AND関数。2の倍数と3の倍数の論理積。

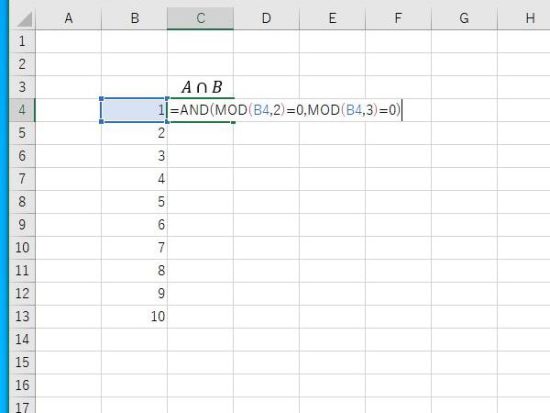
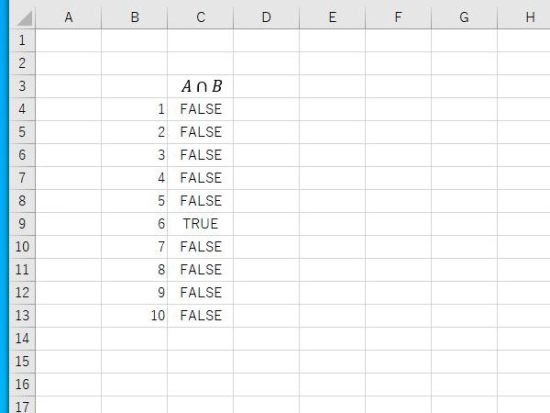
AND関数の結果。2の倍数かつ3の倍数なので 6が該当します。

法則1の左辺。(AかつB)ではないは、ANDの結果をNOTで否定。

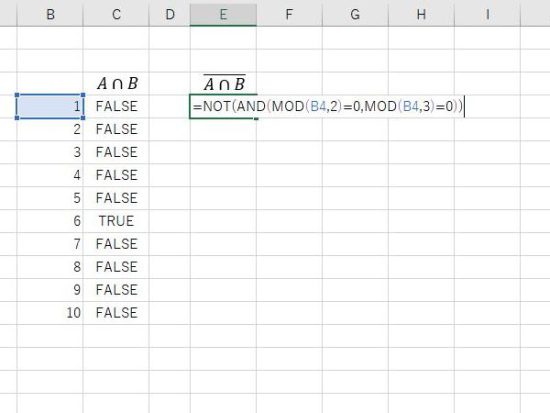
結果の表示。6はFALSEとなり、それ以外がTRUEとなります。

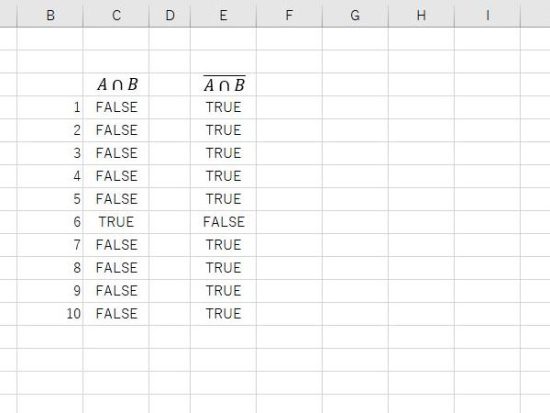
法則1の右辺。(Aではない)または(Bではない)は、(それぞれの引数の否定)の OR。

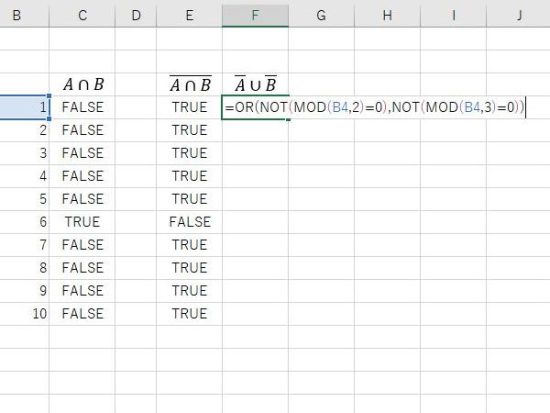
結果の表示。法則1の左辺と右辺は、同じ結果になります。

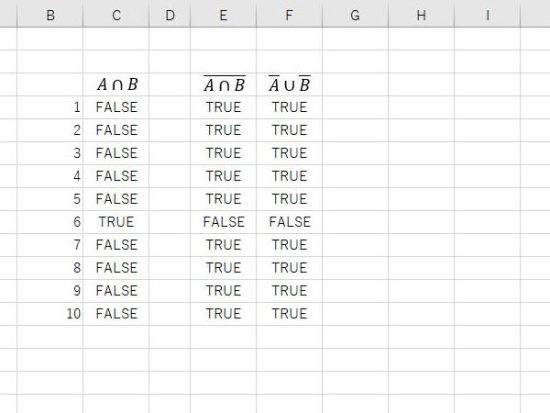
IF関数での表示。

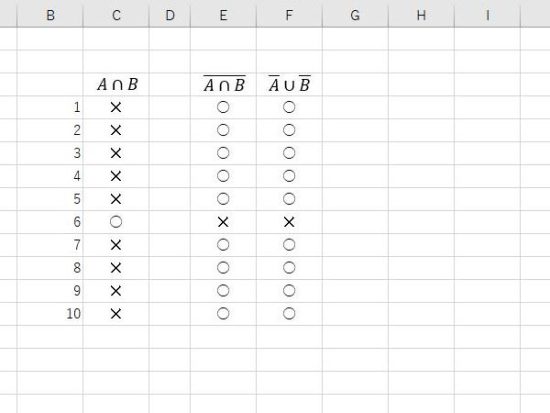
OR関数。2の倍数と3の倍数の論理和。

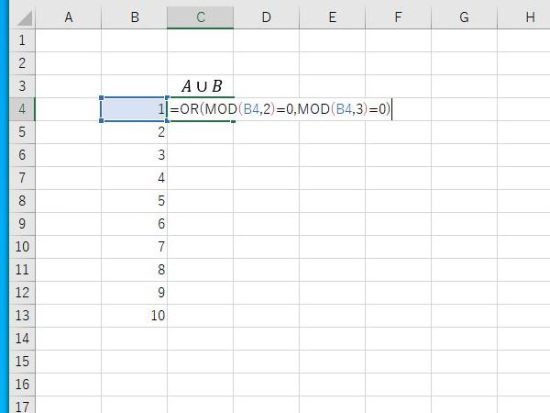
OR関数の結果。2の倍数または3の倍数なので 2、3、4、6、8、9、10が該当します。

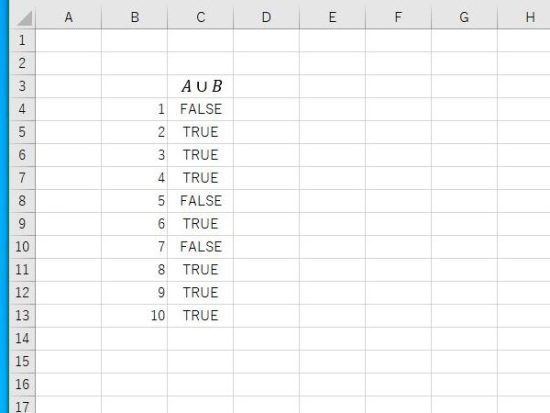
法則2の左辺。(AまたはB)ではないは、ORの結果をNOTで否定。

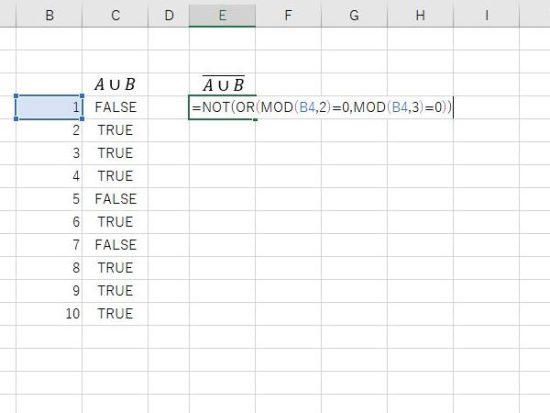
結果の表示。2、3、4、6、8、9、10はFALSEとなり、1、5、7がTRUEとなります。

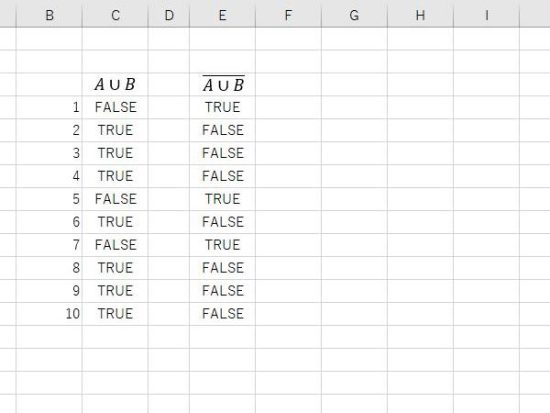
法則2の右辺。(Aではない)かつ(Bではない)は、(それぞれの引数の否定)のANDになります。

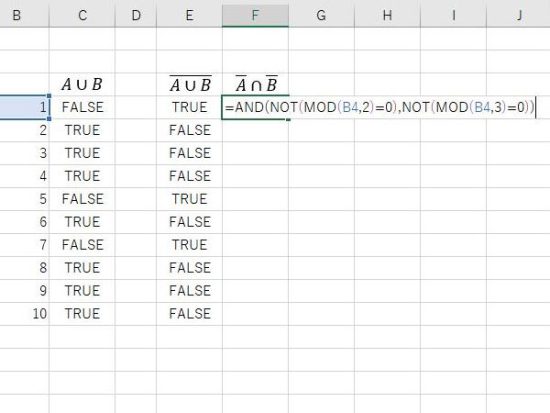
結果の表示。法則2の左辺と右辺は、同じ結果になります。

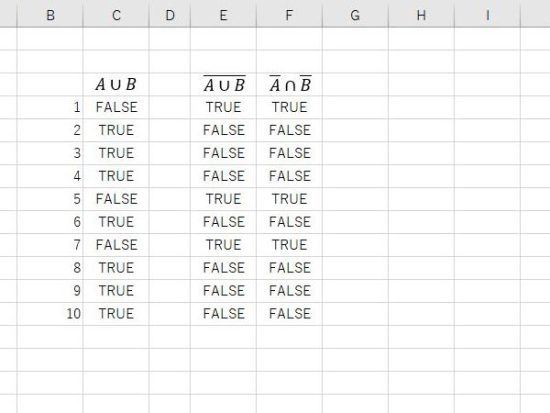
IF関数での表示。

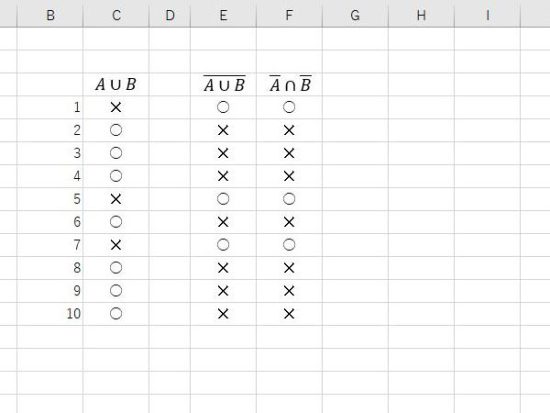
論理演算は、半導体の基本的な回路としても使われており、ド・モルガンの法則が応用されています。

法則1の左辺 (AかつB)ではないは、ANDの否定(AND-NOT)でNAND、法則2の左辺 (AまたはB)ではないは、ORの否定(OR-NOT)で NORといいます。

NANDの入力値を否定したもの(NOT-AND-NOT)は OR、NORの入力値を否定したもの(NOT-OR-NOT)は ANDになります。

半導体はその性質・特徴から、NANDが基本回路として使われることが多くなっています。つまり、NANDの否定でAND、NANDの入力値の否定でOR、ORの否定からNORとなります。またNOT・AND・ORを組み合わせるとXORにすることができます。