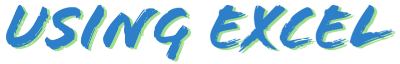NORM.DIST関数（正規分布の確率）

ノーマル・ディストリビューション

NORM.DIST関数は、正規分布の確率を返す関数です。正規分布とは、単峰・左右対称の形状をした確率分布モデルのこと。正規分布モデルともいいます。

引数には、データの値（x）、平均、標準偏差、関数形式の4つを使います。関数形式は、累積分布関数がTRUE（1）、確率密度関数がFALSE（0）。

例：NORM.DIST関数を入力。データの値20、平均25、標準偏差7、累積分布関数を指定。

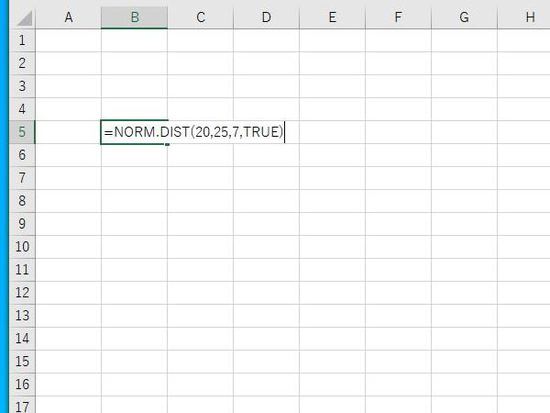
Enterで結果が表示されます。累積分布関数なので下側確率であり、0.237525、約23.8%。xが20以下の値をとる確率となります。

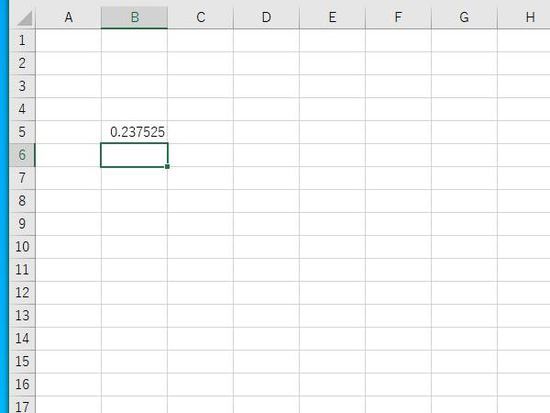
例：同様に関数を入力。第4引数に確率密度関数を指定。

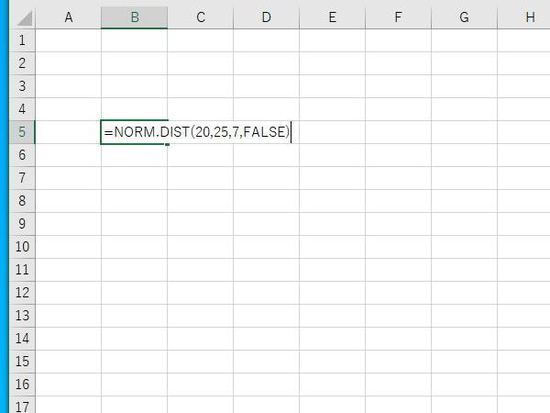
Enterで結果が表示されます。

一般的に正規分布では、累積分布関数を用いることが多くなっています。

累積分布関数を用いると、下側確率の他、区間確率、上側確率を求めることができます。

例：B5にデータの値20、B6にデータの値15を指定。B5からB6の累積分布関数の値を引くと 区間確率になります。

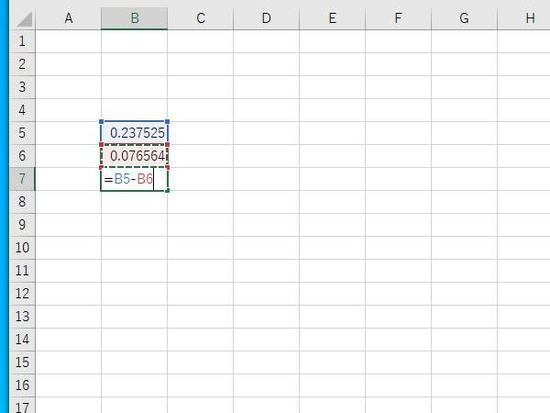
Enterで結果が表示されます。xの値が15から20をとる確率は約16%となります。正規分布では、全体の面積を1（100%）としたときに、Xの値が15から20における面積は0.16（16%）です。

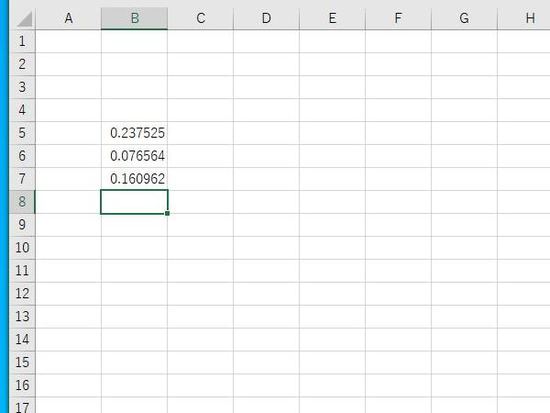
例：B5にデータの値40を指定。B7で1からB5の値を引くと 上側確率になります。

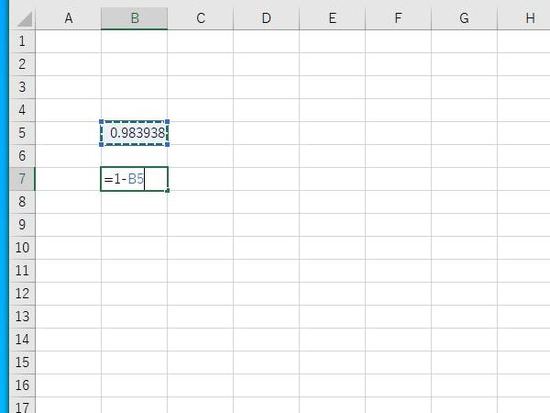
Enterで結果が表示されます。xの値が40以上をとる確率は約1.6%となります。

正規分布は、平均 μ（ミュー）と標準偏差 σ（シグマ）によってその形状が変化します。

標準偏差が小さければ、平均にデータが集まり 中心が高い形状、標準偏差が大きければ中心が低くデータが左右に広がった形状となります。またどのような形状になっても、正規分布の面積は1（100%）として考えることができます。

平均0、標準偏差1の正規分布は、標準正規分布といいます。NORM.DIST関数では、第2引数に0、第3引数に1と指定すると、標準正規分布での確率となります。また、標準正規分布における確率を返す関数に、NORM.S.DIST関数があります。