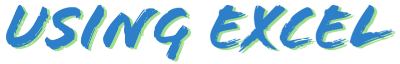変動係数（CV）

変動係数は、CV（coefficient of variation）、相対標準偏差ともいいます。異なるデータのばらつき（変動の度合い）を比較することができます。

例：数式を入力。B16に標準偏差、B14に平均。標準偏差はホーム→小数点第3位まで表示。変動係数は、標準偏差/平均で求めることができます。

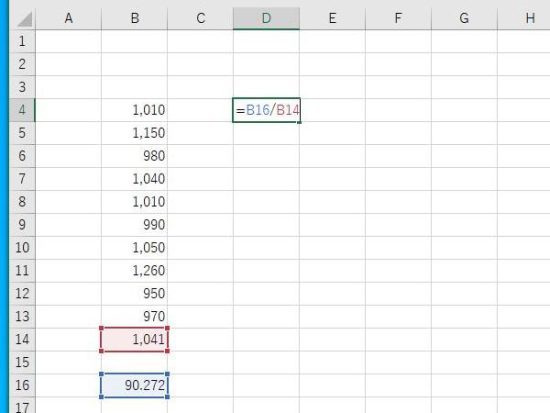
Enterで結果が表示されます。ホーム→小数点第3位まで表示。変動係数は0.087で8.7%になります。

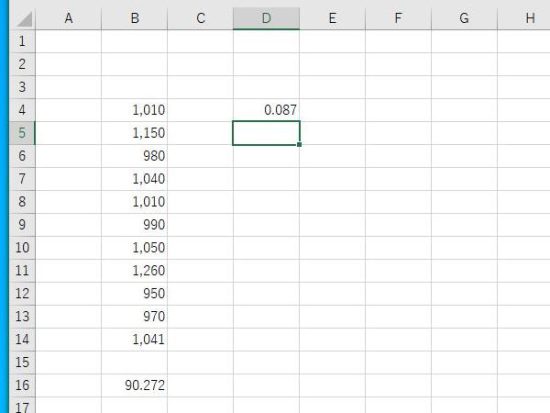
例：数式を入力。B16に標準偏差、B14に平均。標準偏差はホーム→小数点第3位まで表示。

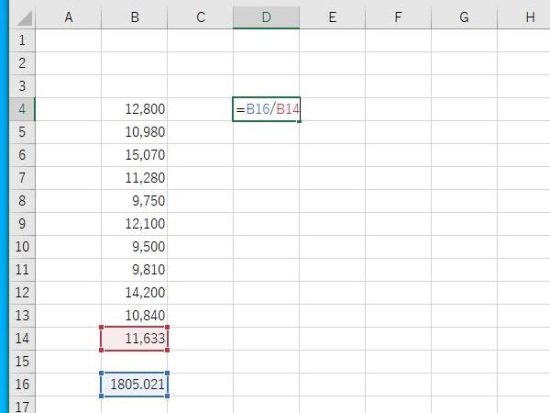
Enterで結果が表示されます。ホーム→小数点第3位まで表示。変動係数は0.155で15.5%になります。

変動係数は、数式にも表されているように 標準偏差の平均に対する割合・比率を求めていることになります。数式を(標準偏差/平均)*100とすることでパーセント表示させることもできます。一般的に変動係数は単位に%が使われることが多くなっています。

標準偏差が近い2つのデータ（B列とC列）の変動係数。

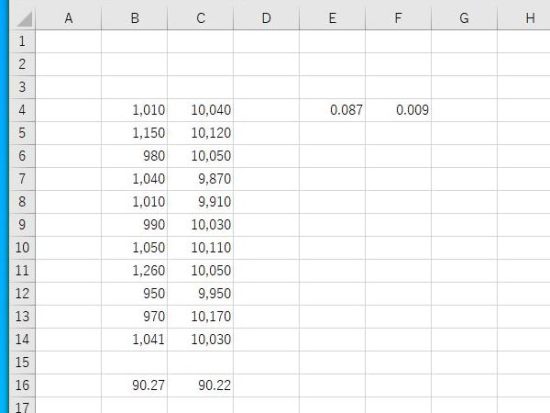
標準偏差が同じような値でも平均が異なるため、変動係数はB列は8.7%、C列は0.9%になります。

B列は、平均1,041に対して標準偏差90.27、C列は平均10,030に対して標準偏差90.22となり、B列の方が数値のばらつきは大きく変動係数は高くなります。つまり変動係数が高いということは、数値のばらつきや変動が大きいということになります。