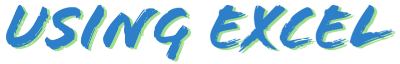BINOM.DIST関数(二項確率)
バイノミアル・ディストリビューション
BINOM.DIST関数は、二項確率を返す関数です。
二項確率とは、ある事象が起きる確率ではなく、起きる確率(成功確率など)が決まっている事象が x回起きる確率です。二項分布、二項分布確率ともいいます。
二項確率は、繰り返しの回数(試行回数)n、成功回数 x、成功確率 pで求めることができます。
引数は4つあり、いずれも省略することはできません。
例:引数に成功回数 2、試行回数 10、成功確率 1/6、関数形式を入力。関数形式は、TRUE(1)が累積分布関数、FALSE(0)が確率密度関数。
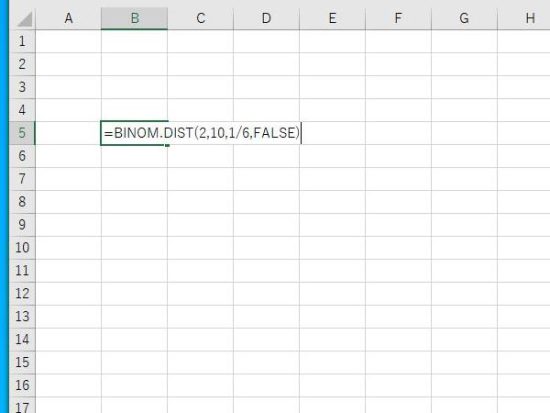
結果の表示。1が100%になります。成功確率 1/6の事象が、10回試行して2回成功する確率は約29%となります。
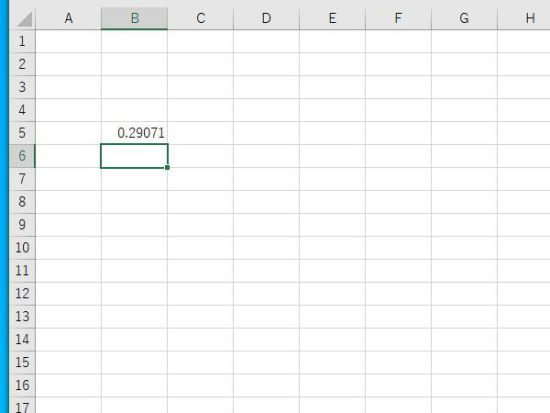
ホーム→数値、標準からパーセントに表示を変更。パーセントは小数点表示にすることもできます。
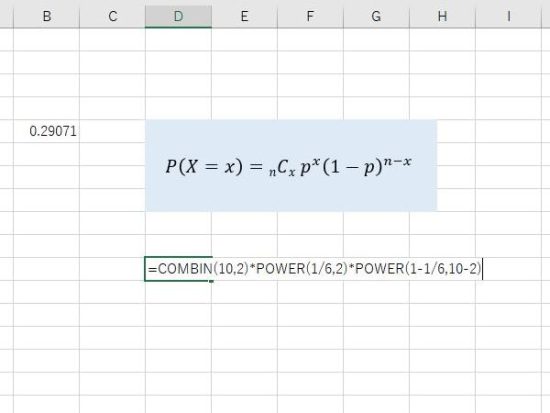
二項確率の数式。nCxは、二項係数ともいいます。Excelでは、COMBIN関数とPOWER関数などでも計算することができます。同じ結果になります。
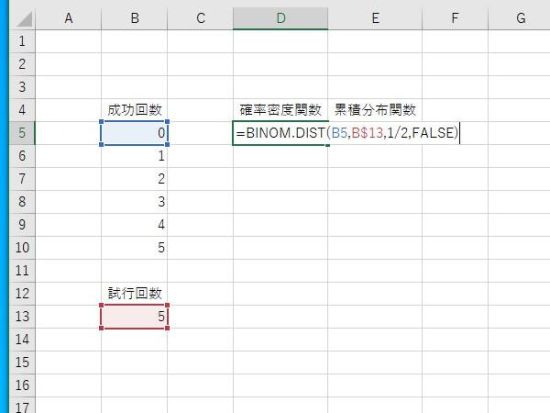
例:引数にセル(成功回数、試行回数)、成功確率、関数形式(FALSE、確率密度関数)を入力。
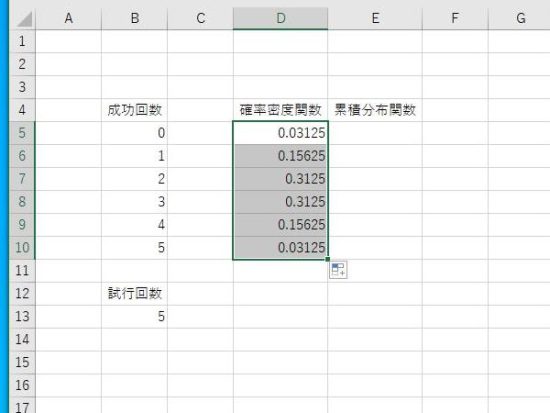
オートフィルの結果。
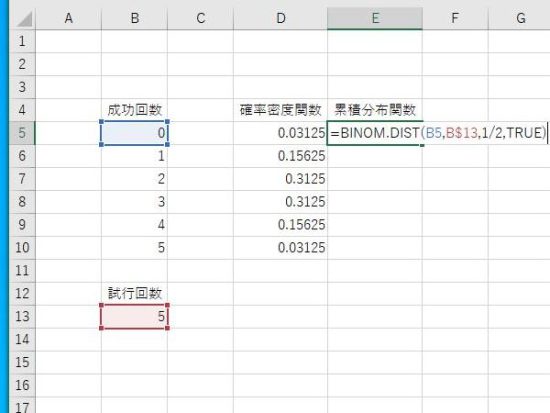
例:引数にセル(成功回数、試行回数)、成功確率、関数形式(TRUE、累積分布関数)を入力。
オートフィルの結果。
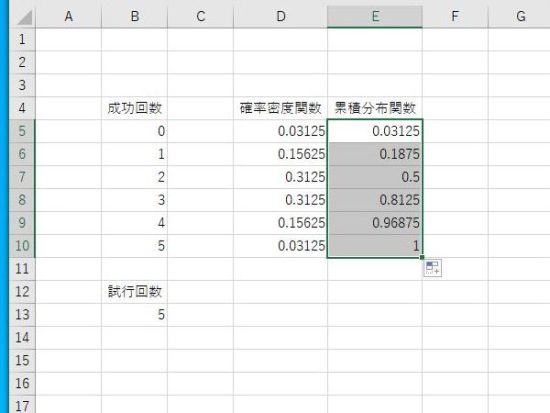
第4引数の確率密度関数と累積分布関数の違い。
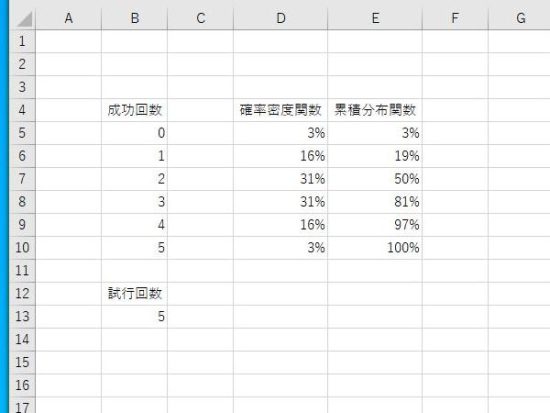
累積分布関数は、確率密度関数で計算された値が累積していることが分かります。例えば、成功回数4では、0~4までのそれぞれの確率密度関数の合計となります。
二項確率は、棒グラフで表示されることがあります。この分布を確率分布や二項分布ともいいます。
成功回数と確率密度関数の数値のある範囲をそれぞれ選択→棒グラフ。また、試行回数と成功確率をセル参照すると、成功確率などを変更してグラフの形状の変化などを確認することができます。
この場合は、D5に =BINOM.DIST(B5,B$18,D$18,FALSE)と入力しています。
試行回数 10、成功確率 1/2(0.5)の確率分布。
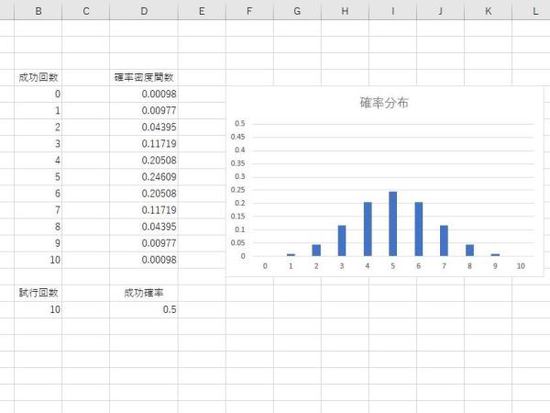
試行回数 10、成功確率 1/10(0.1)の確率分布。
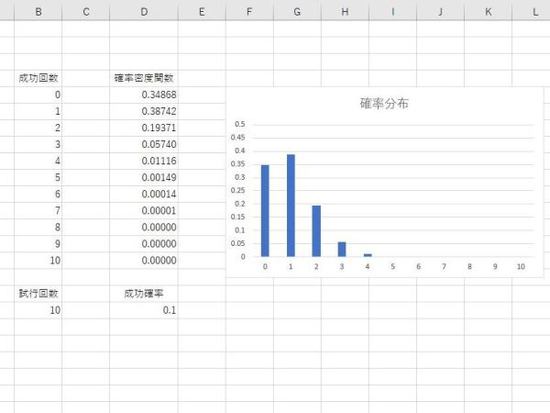
二項分布は、試行回数 nと成功確率 pで決まります。
成功確率 1/2の場合は、左右対称、成功確率が0に近いほど右に歪む(右に裾をひく)、1に近いほど左に歪む(左に裾をひく)という特徴があります。
また、試行回数 nと成功確率 pから以下の値を算出することができます。
- 平均・・np
- 分散・・np(1-p)
- 標準偏差・・np(1-p)の平方根(ルート)
例えば、試行回数10、成功確率0.5であれば、平均5、分散2.5、標準偏差1.5811(小数点第4位まで)となります。分散が最も大きな値(2.5)をとるのは、成功確率0.5のときです。