四分位分散係数

四分位分散係数は、データの中心付近のばらつき（分散の度合い）を表す指標です。異なるデータで比較することもできます。

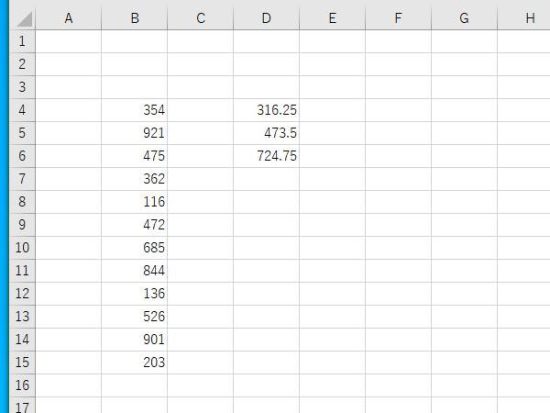
例：データと四分位数。D4に第1四分位数、D5に中央値（第2四分位数）、D6に第3四分位数。四分位数は、QUARTILE.INC関数かQUARTILE.EXC関数を使います。この例では、QUARTILE.INC関数を使用。

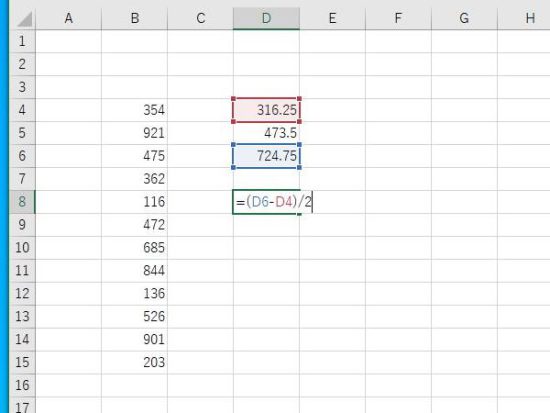
四分位分散係数は、四分位偏差/中央値で求めることができます。四分位範囲は 第3四分位数-第1四分位数、四分位偏差は 四分位範囲/2となります。

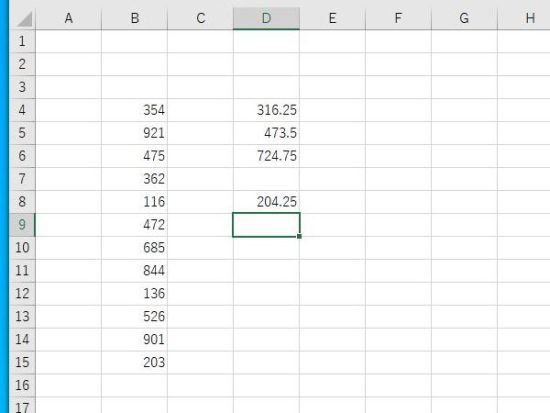
四分位偏差が表示されます。

四分位偏差を中央値で割ります。

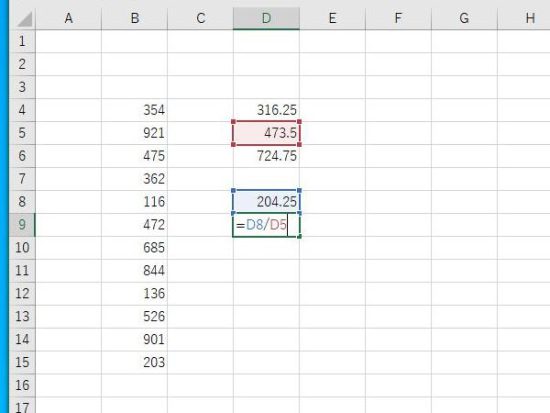
四分位分散係数が表示されます。ホーム→小数点第2位まで表示。

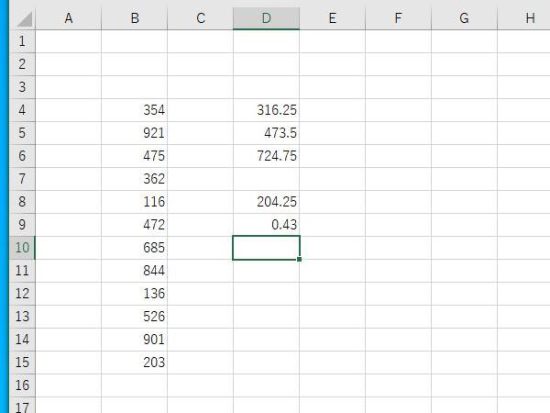
四分位分散係数は、数式にも表されているように 四分位偏差の中央値に対する割合・比率を求めていることになります。四分位偏差は四分位範囲/2であるため、全体的に四分位範囲が大きいほど四分位分散係数も高くなる傾向があります。四分位分散係数が高いほど、中心付近（第1四分位数～第3四分位数）でデータのばらつきが大きいといえます。

また四分位分散係数は、第1四分位数より下、第3四分位数より上にある値を使わない、平均値ではなく中央値を使うなど、外れ値などのデータの影響を受けにくく、中心付近のデータの傾向を確認しやすいという特徴があります。